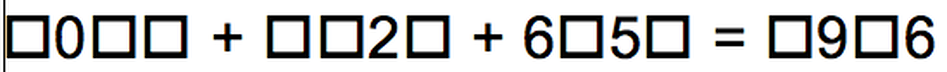Division (1 digit divisor and up to 2 digit dividend)
I understand the meaning of division.
I understand that division and multiplication are related.
Open Question:
Practice/Game:
LOVE THOSE LEFTOVERS!
1. Player 1 rolls two dice and makes a 2-digit number. (Example: if I roll a 2 and a 3, my number can be 23 or 32).
2. Player 1 then rolls one die and uses that number to divide the first number by. (Example: I now roll a 5 and have to divide the number I chose in step 1 by 5. 23÷5 or 32÷5).
3. Player 1 records their division question and solves it. (Example: 23÷5 = 4 with a remainder of 3).
4. Players take 5 turns each. After five turns each player adds up all of their remainders and whoever has the greatest number wins.
LOVE THOSE LEFTOVERS!
1. Player 1 rolls two dice and makes a 2-digit number. (Example: if I roll a 2 and a 3, my number can be 23 or 32).
2. Player 1 then rolls one die and uses that number to divide the first number by. (Example: I now roll a 5 and have to divide the number I chose in step 1 by 5. 23÷5 or 32÷5).
3. Player 1 records their division question and solves it. (Example: 23÷5 = 4 with a remainder of 3).
4. Players take 5 turns each. After five turns each player adds up all of their remainders and whoever has the greatest number wins.
Stretch Your Learning:
Broken Keys Problem: The division key on their calculator has broken. How can you use it to find the answer to 95 ÷ 7? Remember to use what you know about multiplication to solve the problem.
Multiplication (2 or 3 digit by 1 digit)
I understand the meaning of multiplication.
I can demonstrate an understanding of multiplication with 2 or 3 digit numbers by 1 digit numbers.
Think: What do I already know that will help me understand multi-digit multiplication?
Think: What do I already know that will help me understand multi-digit multiplication?
Warm-up:
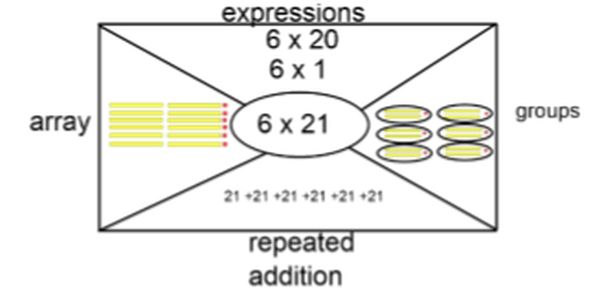
Represent an equation in multiple ways.
Look at the example below and then try representing the equation: 5 x 37 in multiple ways
Represent an equation in multiple ways.
Look at the example below and then try representing the equation: 5 x 37 in multiple ways
Lesson:
1) Watch these videos to explore some strategies for multiplying 2 digit numbers by 1 digit numbers.
1) Watch these videos to explore some strategies for multiplying 2 digit numbers by 1 digit numbers.
|
|
|
2) Look at the multiplication equations below. and build or draw an array to represent each equation.
a. 31 x 7
b. 66 x 5
3) Fill in the missing numbers to complete the equation.
a. 31 × 7 = (30 × 7) + (___ × 7)
b. 66 × 5 = (___ × 5) + (6 × 5)
Problem Solving: The students are trying to collect 150 marbles for the competition on Saturday. They have collected 5 bags. There are 26 marbles in each bag. How many marbles have they collected? Have they reached their goal? Solve and show your thinking.
Practice:
a. 31 x 7
b. 66 x 5
3) Fill in the missing numbers to complete the equation.
a. 31 × 7 = (30 × 7) + (___ × 7)
b. 66 × 5 = (___ × 5) + (6 × 5)
Problem Solving: The students are trying to collect 150 marbles for the competition on Saturday. They have collected 5 bags. There are 26 marbles in each bag. How many marbles have they collected? Have they reached their goal? Solve and show your thinking.
Practice:
Snap Multiplication
Goal: To create the lowest product
Materials: a deck of cards (face cards removed)
How to Play:
1. The goal is to create the lowest possible product.
2. Player One takes three cards from the deck.
3. He/she selects two of the cards to make a 2-digit number and writes it down.
4. He/she multiplies that 2-digit number by the value of the third card,
5. Player Two checks the product on a calculator. If the product is complete, Player One gets 2 points.
6. The steps are repeated for Player Two’s turn.
7. The player who got the lowest product for that round gets 5 points.
Stretch Your Learning
Sometimes when you multiply a 2-digit by 3, you get a 3-digit number.
Goal: To create the lowest product
Materials: a deck of cards (face cards removed)
How to Play:
1. The goal is to create the lowest possible product.
2. Player One takes three cards from the deck.
3. He/she selects two of the cards to make a 2-digit number and writes it down.
4. He/she multiplies that 2-digit number by the value of the third card,
5. Player Two checks the product on a calculator. If the product is complete, Player One gets 2 points.
6. The steps are repeated for Player Two’s turn.
7. The player who got the lowest product for that round gets 5 points.
Stretch Your Learning
Sometimes when you multiply a 2-digit by 3, you get a 3-digit number.
- How many of these numbers are there?
- Which 2-digit is the smallest?
- Which one is the greatest?
Use Personal Strategies to Solve Subtraction Problems
I can use personal strategies for subtracting 3 and 4 digit numbers.
Warm up:
Use mental math to solve 81-26=____.
Explain your personal strategy. Record your thinking so someone else would understand.
Watch the video link below to see if someone used the same strategy as you. How did the students break up 26 to help them solve the problem? How did they use a number line to show their thinking? Why did one student use 85-30 to solve 81-26?
Use mental math to solve 81-26=____.
Explain your personal strategy. Record your thinking so someone else would understand.
Watch the video link below to see if someone used the same strategy as you. How did the students break up 26 to help them solve the problem? How did they use a number line to show their thinking? Why did one student use 85-30 to solve 81-26?
Lesson:
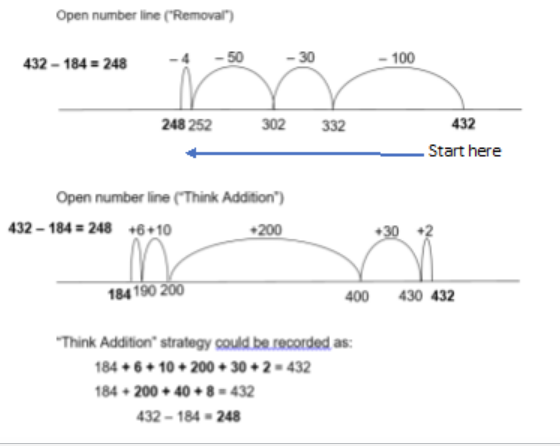
Maria has scored 432 points playing her favourite video game. She used 184 points to get new tools in the game. How many points does she have left?
Use a personal strategy to solve this problem.
Below are examples of how 3 students showed their thinking.
Maria has scored 432 points playing her favourite video game. She used 184 points to get new tools in the game. How many points does she have left?
Use a personal strategy to solve this problem.
Below are examples of how 3 students showed their thinking.
Practice:
Game #1: First to Zero
How to Play:
Game #2: Four Strikes and You're Out
This game is played with the same rules as Hangman, with the only difference being the use of numbers instead of letters. You may recognize this game from a few weeks ago, but this time we are playing using subtraction.
How to Play:
Stretch Your Learning:
Open Question: Two numbers are both more than 1000. The difference between them is 3839.
- What could the numbers be?
- What could the numbers be if the ones digit of the greater number is 2?
- What could the numbers be if the ones and the tens digit of the greater number are both 3?
- What could the numbers be if the ones digit of the least number is 7?
Game #1: First to Zero
How to Play:
- First, on a sheet of paper, each player needs to write the players' names and the number 999 under them.
- A player rolls the three dice, then arranges the three numbers (for example, 2, 3, 5) in some order (for example, 235, 352, 532, and so on) and subtracts that 3-digit number from 999. the other players also should check the players work.
- The players take turns, rolling the die to make their special number and subtracting that number from their total.
- The winner is the first player to reach 0, but they must get to 0 exactly. At any time, a player may choose to roll only on or two dice , instead of three dice. If the only numbers a player can make are larger than their remaining score, the player loses their turn.
Game #2: Four Strikes and You're Out
This game is played with the same rules as Hangman, with the only difference being the use of numbers instead of letters. You may recognize this game from a few weeks ago, but this time we are playing using subtraction.
How to Play:
- Player 1- creates a subtraction number sentence on a piece of paper. You can use 2, 3, or 4-digit numbers. For example, 564 – 125= 439 (Don't show your partner your equation!). On a second piece of paper write the following: _ _ _ - _ _ _ = _ _ _ and write 0 1 2 3 4 5 6 7 8 9 underneath the equation.
- Player 2 - take turns guessing numbers to go in the blanks. If the number is in the equation, Player 1 writes the number in the correct blank (if there are multiples of that number, write them all in). If the number is not in the equation that is one strike. If Player 2 makes 4 incorrect guesses (strikes) Player 1 wins. If Player 2 correctly figures out Player 1's equation, Player 2 wins. When this round is over, switch roles.
Stretch Your Learning:
Open Question: Two numbers are both more than 1000. The difference between them is 3839.
- What could the numbers be?
- What could the numbers be if the ones digit of the greater number is 2?
- What could the numbers be if the ones and the tens digit of the greater number are both 3?
- What could the numbers be if the ones digit of the least number is 7?
Use Personal Strategies to Solve Addition Problems
I can use personal strategies for adding 3 and 4 digit numbers.
Warm up:
Use mental math to solve 49+29=____.
Explain your personal strategy. Record your thinking so someone else would understand.
Watch the video below to see if someone used the same strategy as you. How did they expand or break up their numbers? What do you think the word compensation means in this video?
Use mental math to solve 49+29=____.
Explain your personal strategy. Record your thinking so someone else would understand.
Watch the video below to see if someone used the same strategy as you. How did they expand or break up their numbers? What do you think the word compensation means in this video?
Lesson:
Ben and his sister Emily have been keeping track of their weekly exercise minutes. Ben has exercised for 364 minutes and Emily has exercised for 128 minutes. How many minutes in total have they exercised?
Use a personal strategy to solve this problem.
Compare your thinking to the thinking of the 4 students below. How is your thinking the same/different?
Ben and his sister Emily have been keeping track of their weekly exercise minutes. Ben has exercised for 364 minutes and Emily has exercised for 128 minutes. How many minutes in total have they exercised?
Use a personal strategy to solve this problem.
Compare your thinking to the thinking of the 4 students below. How is your thinking the same/different?
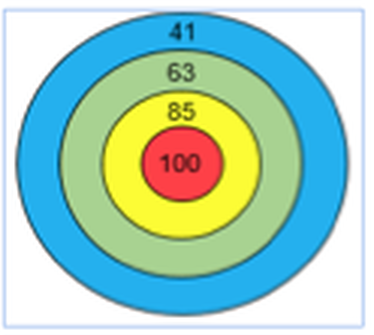
Practice: "Dartboard Addition"
Use the dartboard below to solve the following problems related to it.
Use the dartboard below to solve the following problems related to it.
- Four darts were thrown at the dartboard and they all hit. The sum was 296. What numbers did the darts land on?
- Some darts were thrown at the dartboard and they all hit. The sum of the numbers was 271. How many darts were thrown? What numbers did they land on?
- What are all of the possible sums if you throw three darts at the board and never miss?
- What other problems can you create using the dartboard?
Game #1: First to 5000
Set up your own dart board with 4, 3-digit numbers. Use a rolled up sock or something soft to throw as your “dart”. Each player would throw 2 socks and record the sum. The player to reach 5000 first is the winner! You could also place the target on the floor or table and toss a counter, ball of paper, sock, etc. on to the target.
Game #2: Name Your Target
Set up your own dart board with 4, 3-digit numbers. Use a rolled up sock or something soft to throw as your “dart”. Each player would throw 2 socks and record the sum. The player to reach 5000 first is the winner! You could also place the target on the floor or table and toss a counter, ball of paper, sock, etc. on to the target.
Game #2: Name Your Target
- Step 1: Sort the deck of cards. Remove Kings, Queens, Jacks and tens. Set those aside because they are not needed for this game.
- Step 2: Shuffle the remaining cards and place them face down in a stack.
- Step 3: Decide who the dealer will be. This is the person who decides the target (goal) of the game for each round and distributes the cards.
- Step 4: The dealer states the target for the round. Example: “Try to rearrange your 3 cards to make an odd number that is as close to 500 as possible”.
- Step 5: The dealer gives each player 3 cards. The players then try to arrange their cards to reach the stated target.
- Step 6: Each person then says how far away they are from the target number.
The person who is closest wins the round. They get a point and become the next dealer.
- Step 7: The game continues in this way until all the cards are used.
To make it a little easier: Use 2 cards instead of 3 and work with lower numbers.
To make it a little harder: Use more cards and larger numbers
Stretch Your Learning:
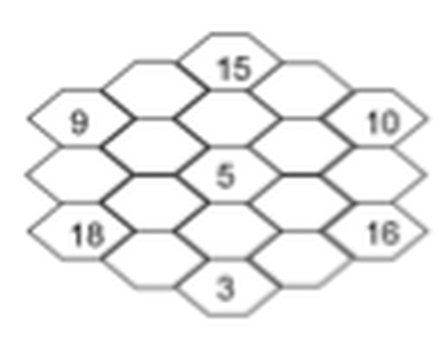
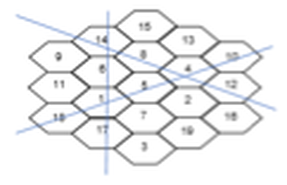
1) Hexagon Puzzle:
This puzzle was created by 19 year-old Clifford Adams over a hundred years ago! To solve the puzzle, fill in the hexagons with the numbers 1 to 19, so that any straight line will add to 38 (vertically or diagonally). It is a challenging puzzle, so seven of the numbers have been already placed correctly.
1) Hexagon Puzzle:
This puzzle was created by 19 year-old Clifford Adams over a hundred years ago! To solve the puzzle, fill in the hexagons with the numbers 1 to 19, so that any straight line will add to 38 (vertically or diagonally). It is a challenging puzzle, so seven of the numbers have been already placed correctly.
2) Open Questions:
Look at the addition equation below. Fill in the blanks using each digit 0 to 9 only once to make the equation true. Show and explain your thinking using models, numbers, words, and/or pictures.
Look at the addition equation below. Fill in the blanks using each digit 0 to 9 only once to make the equation true. Show and explain your thinking using models, numbers, words, and/or pictures.
Solution for the Hexagon Puzzle:
About How Much
Warm up:
Lesson:
1. Look at the rectangle below. How much of it is shaded?
- How many ways can you represent the fraction ½?
- Try this before moving on to the lesson.
Lesson:
1. Look at the rectangle below. How much of it is shaded?
If you said ½ (half) or 3/6, than you are on the right track!
2. If I shade a bit more of the rectangle in, about how much of the rectangle is now shaded?
2. If I shade a bit more of the rectangle in, about how much of the rectangle is now shaded?
It is still about 3/6 but what could we do if we wanted a closer estimate?
What if we divide the pieces in half to form twelfths? Have a look at the rectangle below. Are we able to get a closer estimate now?
What if we divide the pieces in half to form twelfths? Have a look at the rectangle below. Are we able to get a closer estimate now?
3. Now look at the rectangle below. How you could get an estimate for the shaded amount? What are some strategies you could use? Give it a try!
Possible strategies:
- Divide the rectangle into equal parts and use those parts to determine an estimate.
- Decide whether the amount is closer to 0, ½, or 1.
- Then you might divide the parts further to see if the amount is closer to 0, ¼ , ½, ¾ , or 1.
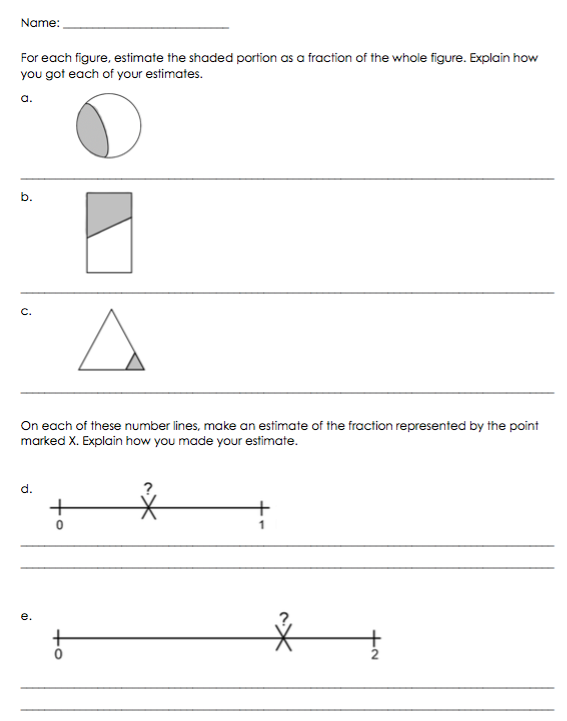
Task: Determine a fraction that you think is a good estimate of the amount shown in each picture on the sheet below. Share your estimate and the way you determined the estimate for each picture.
| fraction_practice.pdf | |
| File Size: | 55 kb |
| File Type: | |
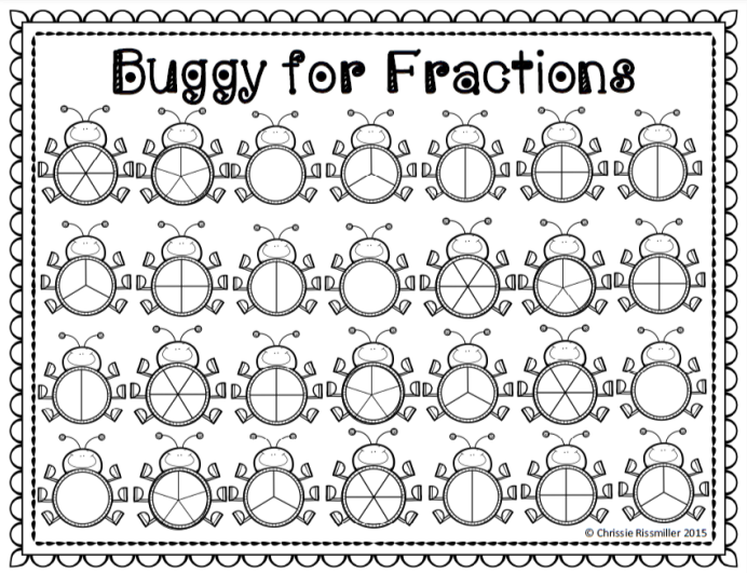
Practice: Buggy for Fractions
The object of the game is to “own” the most bugs. A player may claim a bug when more than half of the fraction has been coloured with their colour. (See below for the game board)
1. Players take turns rolling the dice. The lower number will be the numerator and the higher number is the denominator. (eg. If you roll a 3 and a 5, your fraction would be 3/5 )
2. The player says the fraction and then colours the fraction on the game board. They may colour all of the fraction on one bug or split the fraction among multiple bugs. (eg. 1/5 and 2/5 )
3. Once a player has coloured more than half of the bug they may put their initials beside the bug to claim it. If a bug is equally coloured, neither player claims that bug.
4. Whoever has the most bugs claimed at the end wins that game.
The object of the game is to “own” the most bugs. A player may claim a bug when more than half of the fraction has been coloured with their colour. (See below for the game board)
1. Players take turns rolling the dice. The lower number will be the numerator and the higher number is the denominator. (eg. If you roll a 3 and a 5, your fraction would be 3/5 )
2. The player says the fraction and then colours the fraction on the game board. They may colour all of the fraction on one bug or split the fraction among multiple bugs. (eg. 1/5 and 2/5 )
3. Once a player has coloured more than half of the bug they may put their initials beside the bug to claim it. If a bug is equally coloured, neither player claims that bug.
4. Whoever has the most bugs claimed at the end wins that game.
| buggys_fraction_game.pdf | |
| File Size: | 308 kb |
| File Type: | |
Stretch Your Learning:
1) Open Ended Question
Think of some fractions where the numerator is 3 less than the denominator (e.g., 2/5 ).
Which of the following statements could be true, and explain your thinking.
2) Rectangle Tangle
https://nrich.maths.org/1048
1) Open Ended Question
Think of some fractions where the numerator is 3 less than the denominator (e.g., 2/5 ).
Which of the following statements could be true, and explain your thinking.
- The fraction is less than 1/2 .
- The fraction is greater than 1/2 .
- The fraction is greater than 3/4 .
- The fraction is greater than 9/10 .
- The fraction is less than 1/8 .
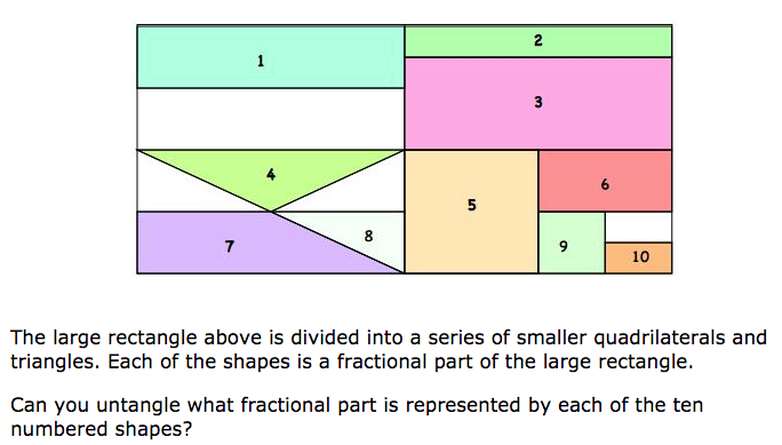
2) Rectangle Tangle
https://nrich.maths.org/1048
Close, Far, and in Between
I can think about the size of numbers.
I can use mental math strategies.
I can use mental math strategies.
Warm-up:
Look at the number line below and answer the questions.
Look at the number line below and answer the questions.
- Which number is closest to 50?
- Which 2 numbers are closet?
- How far apart are 27 and 100?
- How far apart are 83 and 100?
- How far apart are 62 and 100?
- What was your strategy?
- Tell me your thinking.
Lesson:
Task #1: Look at the number line below and answer the questions.
Task #1: Look at the number line below and answer the questions.
- Which two numbers are closest? Why?
- Which number is closet to 300?
- Which number is closest to 250?
- About how far apart are 219 and 500?
- About how fart apart are 219 and 5000?
Task #2: Look at the number line below and draw one just like it. Then, make up cards with the following numbers and place them on your number line: 2345, 5010, 8341, 6999.
- Which two numbers are closest? Why?
- Which number is closet to 3000?
- Which number is closest to 2500?
- About how far apart are 2345 and 5010?
- About how fart apart are 2345 and 10 000?
- What was your strategy?
- Tell me your thinking.
Practice: 4-Digit "Trash Can"
Students play against a partner to try to create the largest number possible.
Materials:
How to Play:
Player 1 rolls the 10-sided die (or draws a card from the bag). They write that number in one of the place value spots on their board, keeping in mind that they are trying to make the largest number possible. · Players take turns rolling and filling in their board, one space at a time. · Students have one opportunity to “throw out” a number and replace it with one that would help them create the largest number. · The player who creates the largest number wins.
If you want to make it harder:
Practice reading your number, then think...
What would ten more be?
What would 100 more be?
What would 100 less be?
What would 2000 more be?
What would 2000 less be?
Students play against a partner to try to create the largest number possible.
Materials:
- Draw a Trash Can game board.
- 10-sided die (If you don’t have a 10-sided die labelled 0-9, record the numbers 0-9 on cards and place them in a bag)
How to Play:
Player 1 rolls the 10-sided die (or draws a card from the bag). They write that number in one of the place value spots on their board, keeping in mind that they are trying to make the largest number possible. · Players take turns rolling and filling in their board, one space at a time. · Students have one opportunity to “throw out” a number and replace it with one that would help them create the largest number. · The player who creates the largest number wins.
If you want to make it harder:
Practice reading your number, then think...
What would ten more be?
What would 100 more be?
What would 100 less be?
What would 2000 more be?
What would 2000 less be?
Stretch Your Learning:
Tamara has eight cards in front of her in this order: 5, 1, 3, 7, 9, 0, 5, and 2. (Each number is on a separate card!)
Which four cards should she take away so that the remaining four cards when pushed together without changing their order would give:
a) the smallest possible 4-digit number
b) the greatest possible 4-digit number
c) the smallest possible 4-digit odd number?
Tamara has eight cards in front of her in this order: 5, 1, 3, 7, 9, 0, 5, and 2. (Each number is on a separate card!)
Which four cards should she take away so that the remaining four cards when pushed together without changing their order would give:
a) the smallest possible 4-digit number
b) the greatest possible 4-digit number
c) the smallest possible 4-digit odd number?
What's going on outside your window?
Pick a window time: It can be 15 minutes or 30 minutes and keep an eye out for what happens. What do you see? Are people walking by? Birds hanging out? How many trees can you see? How can you collect your data? Maybe tally marks? How can you represent your data? Find a way to visualize the information you collect. Maybe a timeline or a chart? Be your most creative self!
So… off you go… Collect data on what you see and report it in a creative visual representation. If time allows, this activity can be repeated through the week.
Watch the video to see examples of what some children did.
So… off you go… Collect data on what you see and report it in a creative visual representation. If time allows, this activity can be repeated through the week.
Watch the video to see examples of what some children did.
Practice: Four Strikes and You're Out (N3)
This game is played with the same rules as Hangman, with the only difference being the use of numbers instead of letters.
Player 1- create an addition number sentence on a piece of paper. You can use 2, 3, or 4-digit numbers. eg. 5643+2752 = 8395 (Don't show your partner your equation!). On a second piece of paper write the following: _ _ _ _ + _ _ _ _ = _ _ _ _ and write 0 1 2 3 4 5 6 7 8 9 underneath the equation.
Player 2- takes turns guessing numbers to go in the blanks. If the number is in the equation, Player 1 writes the number in the correct blank (if there are multiples of that number, write them all in). If the number is not in the equation that is one strike.
How to win: If Player 2 makes 4 incorrect guesses (strikes) Player 1 wins. If Player 2 correctly figures out Player 1's equation, Player 2 wins. When this round is over, switch roles.
Stretch Your Learning:
Two numbers are both more than 1000. The difference between them is 3839. What could the numbers be?
What could the numbers be if the ones digit of the greater number is 2?
What could the numbers be if the ones and tens digit of the greater number are both 3? Sample: 2500 and 6339
This game is played with the same rules as Hangman, with the only difference being the use of numbers instead of letters.
Player 1- create an addition number sentence on a piece of paper. You can use 2, 3, or 4-digit numbers. eg. 5643+2752 = 8395 (Don't show your partner your equation!). On a second piece of paper write the following: _ _ _ _ + _ _ _ _ = _ _ _ _ and write 0 1 2 3 4 5 6 7 8 9 underneath the equation.
Player 2- takes turns guessing numbers to go in the blanks. If the number is in the equation, Player 1 writes the number in the correct blank (if there are multiples of that number, write them all in). If the number is not in the equation that is one strike.
How to win: If Player 2 makes 4 incorrect guesses (strikes) Player 1 wins. If Player 2 correctly figures out Player 1's equation, Player 2 wins. When this round is over, switch roles.
Stretch Your Learning:
Two numbers are both more than 1000. The difference between them is 3839. What could the numbers be?
What could the numbers be if the ones digit of the greater number is 2?
What could the numbers be if the ones and tens digit of the greater number are both 3? Sample: 2500 and 6339
Multiplication
I understand the meaning of multiplication.
Practice:
- Practice representing 5 x 7 in different ways. Use my sample below to help give you some ideas of ways you can represent the fact. Try another fact for more practice.
- Look through the Concentration game cards (see attachment below). Lay all the cards out facing up and practice matching some pairs before playing the game. Explain why you know the cards are equivalent.
Games:
1) Concentration Game
Materials:
2) Tic-Tac-Toe
Materials:
1) Concentration Game
Materials:
- Print and cut out 42 cards provided (see attachment below), or if there is not a printer available you could use recipe type cards to recreate the multiplication cards (no expectation to understand 7² or 8². You may remove these cards).
- Play Concentration using Multiplication Cards. Shuffle and place all of the cards face down. Take turns turning over 2 cards at a time. If the cards match, the player collects them and turns over another pair. If the cards do not match, they are turned back over and another player takes a turn.
2) Tic-Tac-Toe
Materials:
- Game Sheet
- Two markers for the bottom row of factors (for example, paper clips)
- Two sets of different markers for each player to cover each product (for example, pennies and nickels)
- Player X and Player O select one factor, 1 – 9 at the bottom of the page and place one of the markers on that factor.
- Player X may move only one of the two markers to a new factor. Player X then places a marker on the grid covering the product of the two factors.
- Player O may move only one marker to make a new product and place their marker on the grid. The markers can both be placed on the same factor. For example 6 x 6 = 36. Players alternate moving one factor marker at a time and continue placing their markers on the grid until a player has marked four products in a row.
- After the game players should discuss their strategies.
| tictactoe_and_concentration.docx | |
| File Size: | 1002 kb |
| File Type: | docx |
Mutliplication (2- or 3-digit by 1-digit)
I understand the meaning of multiplication.
I can use personal strategies for multiplication.
I can use personal strategies for multiplication.
Ideas of strategies to solve:
Practice Questions:
Game: Uno Multiplication!
- Use Base Ten Blocks to model the problem.
- Use expanded form.
- Break a number apart to multiply.
Practice Questions:
- Multiply. What Patterns do you see? a) 2 x 99 b) 3 x 99 c) 4 x 99 d) 5 x 99 e) 6 x 99
- Find each product. a) 43 x 8 b) 9 x 37 c) 5 x 72 d) 36 x 6 e) 7 x 17 f) 3 x 492 g) 152 x 7 h) 5 x 215
- Find each missing number. a) 178 x 5 = (100 x __) + (70 x 5) + (8 x __) b) 523 x 4 = (500 x 4) + (20 x __) + (__ x 4)
Game: Uno Multiplication!
Fractions on a Number Line
We have not talked too much about fractions yet in class. Here is a little mini-lesson on putting fractions on a number line to help you with Thursday's choice board.
Math Choice Board
There is a Math activity for each day of the week covering a wide range of outcomes. Can you complete all the tasks in 5 weeks? I am posting a warm-up, grade-level, and stretch option for each day. Have fun!
COMING SOON!
Essential Skills
This website includes many different subject areas. Please start by completing the Math 'Pretest'. There is a pretest for each Math section (e.g. Problem Solving, Math Operations, Number Concepts) that needs to be completed. Parents: Please do your best not to help your students with the pretest as it is assessing what the students know. The program then designs lessons that target areas where students may need more practice. I have sent a copy of your students username and password to your email.
Prodigy
Please contact me if you need your login information.